※アフィリエイト広告を利用しています。

今回は、「対応があるノンパラメトリックな多重比較検定を行いたいのですが、どこにも記載されていません。どうしたら良いですか?」という質問に答えたいと思います。
対応があるノンパラメトリックな多重比較検定の方法
対応があるノンパラメトリックな多重比較検定の方法は、ズバリ、Bonferroni法で調整を行うことです。
私自身も様々な本や論文を確認しましたが、対応があるノンパラメトリックな多重比較検定はほとんど記載されていません。
対応がないノンパラメトリックな多重比較検定は、Kruskal-Wallis法を用いて、何らかの差があればSteel-Dwass法でどこに差があるかを確認します。
一方で、対応があるノンパラメトリックな多重比較検定は、Friedman検定を用いて、何らかの差を確認します。
これで、何らかの差があるということまでは確認できます。
しかし、そのあとの多重比較については言及されていません。
そこで、今回、いろいろと調べましたので紹介します。
(対応があるノンパラメトリックな多重比較検定以外については、今回は割愛させてもらいます。)
対応がある?対応がない?
例えば、ネズミにある運動を行わせる実験で、運動前、運動中、運動後のパラメータを測定し、ある運動が影響を与えたかどうかを検定する場合、運動前、運動中、運動後は同じネズミからデータを取得しているので、「対応がある」となります。
一方で、異なる群に運動を行わせる実験で、ネズミ群、サル群、イヌ群のパラメータを測定し、ある運動が各群で影響を与えたかどうかを検定する場合、ネズミ群、サル群、イヌ群は異なる群からデータを取得しているので、「対応がない」となります。
パラメトリック?ノンパラメトリック?
パラメトリック検定は母集団のデータの分布が正規分布と仮定されています。
ノンパラメトリック検定は母集団の分布に仮定がされていない。(仮定がないなので、ノンパラメトリック検定には母集団が正規分布している場合も含まれるということになります。つまり、ノンパラメトリック検定のほうが応用範囲が広くなります。)
分布が傾いていたり、バラツキがあっても可能で、順序尺度にも用いることができます。
多重比較を行う意味は?
多重比較なんて行わなくても、各群の差を複数回に分けて検定したらいいじゃないか。
と思う場合があるかもしれません。
しかし、これはダメです。
なぜ、ダメなのかというと検定を繰り返してしまうと本来の有意水準よりも上昇してしまうことになるからです。
これを、”多重性による第1種の過誤の増大”といいます。
簡単に例を示します。
ある母集団から3群を取り出して、それぞれの平均値をX1、X2、X3とします。
これら3群でそれぞれ差を比較すると、差の検定は、(X1 – X2)×(X1 – X3)×(X2 – X3)の3回行うことになります。
具体的に確率を計算すると、3群で3回検定を行うと、有意とならない確率は(1 – 0.05)× (1 – 0.05)× (1 – 0.05)= 0.86となり、有意水準が14% に上昇してしまいます。
本来は、有意水準5%としたつもりが、検定を繰り返すうちに有意水準が14%になってしまうということです。
そこで、この問題を解決するために考えられたのが多重比較です。
最も単純でわかりやすいのがBonferroni法です。
たとえば3群の場合、差の検定は3回行う必要があるので、単純に有意水準0.05を3で割って、0.017を有意水準とします。
これにより、3回検定しても全体の有意水準は0.05に保つことができるというわけです。
統計ソフトでBonferroni法を選択すれば、この計算を自動で行なってくれます。
Friedman検定の後に、Bonferroni法で調整する
対応があるノンパラメトリックな多重比較検定は、Friedman検定を用いて、まずは何らかの差を確認します。
これで、何らかの差があるということまでは確認できます。
そして、次にどの群とどの群で差があるかを確認するためにBonferroni法で調整して比較を行います。
ただし、比較する群が多くなるほど検出力が低下(有意差が出にくくなる)しますので注意が必要です。
(有意差があることが研究結果の全てではありません。サンプルサイズや効果量なども考慮していく必要があると考えます。)
SPSSで検定を行う手順
①SPSSを起動させて、データを準備します。
②分析(A)→ノンパラメトリック検定→対応のあるサンプル
③”目的”で分析のカスタマイズを選択します。
④”フィールド”で分析したいデータを選択します。(例:介入前の握力、介入3ヶ月後の握力、介入6ヶ月後の握力など)
⑤”設定”で検定のカスタマイズを選択し、Friedmanにチェックします。そして、複数の比較ですべてのペアごとを選択します。
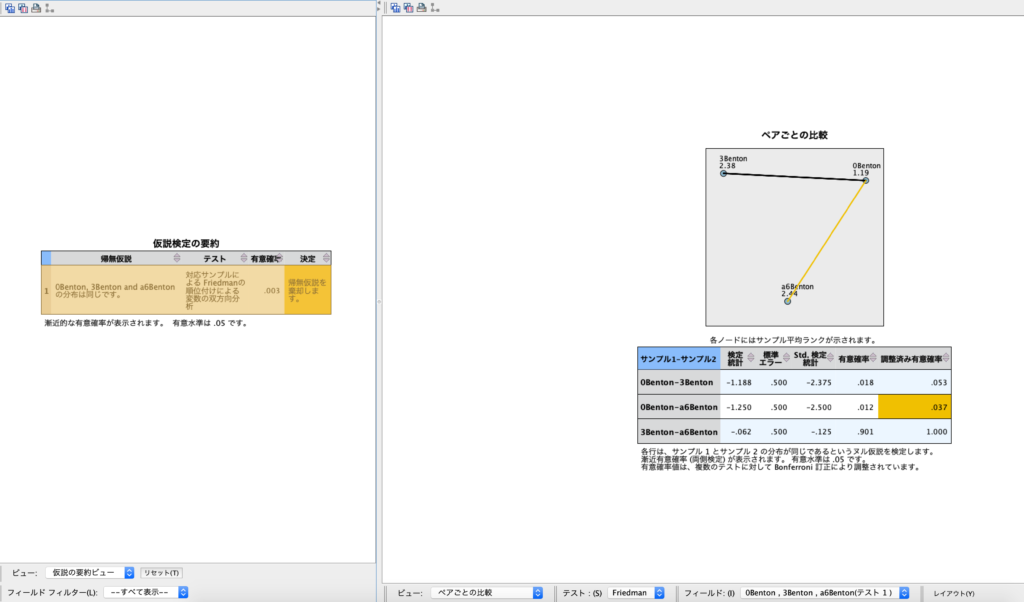
⑥すべて整えば、実行を選択します。すると結果が出てきますので、有意確率が0.05以下であった場合には、多重比較が行われていますので、ダブルクリックします。
⑦右側の左下にある”ビュー”を選択し、ペアごとの比較をクリックすると、Boferroni法で調整した有意確率が表示されます。
詳しい手順については、「SPSSによる分散分析と多重比較の手順」が参考になります。私は、いくつもの書籍や文献を確認しましたが対応があるノンパラメトリックな多重比較検定の手順が記載されている本はこちらの本のみでした。
ポストホックテストについて
ポストホックテストとは、3群以上の多群の差の検定で分散に差があった場合に、さらに個々の群間の差を調べる場合に用いる検定法の総称です。
Bonferroni法:群数が増えるほどに検出力が低くなります。対応がある場合にも使用することが可能であることから、適用範囲が広いのが特徴です。
Scheffe法:群のデータ数、分散、分布に制限なく検定できますが、検出力でやや劣ります。
Fisher’sPLSD法:各群のデータ数が等しく、当分散で正規分布していると仮定して検定を行う。検出力が最も優れているが甘い検定になってしまう危険があります。また、多重性が考慮されていないため、3群のみに限定されます。
その他:Tukey法やDunnett法など
参考資料
石村貞夫・他:SPSSによる分散分析と多重比較の手順
浜田知久馬:学会・論文発表のための統計学
並木昭義:コ・メディカルのための統計学入門
池田郁男:統計検定を理解せずに使っている人のためにⅢ.生物と化学 51(7),2013.
今回は、「対応があるノンパラメトリックな多重比較検定を行いたいのですが、どこにも記載されていません。どうしたら良いですか?」に対して、Friedman検定の後に、Bonferroni法で調整して比較しましょう。と回答させていただきます。